Tips matemáticos de geometría para programación de videojuegos

A la hora de programar un videojuego (o muchos proyectos de corte más visual/interactivo) es casi imposible que no necesitemos echar mano de ciertas fórmulas matemáticas (más concretamente geométricas) para comparar las posiciones relativas de nuestros elementos gráficos en la pantalla. La geometría en dos dimensiones es relativamente sencilla pero aún así en este post presento un ejemplo que sin ser muy complicado echa mano de una serie de fórmulas que quizás no recordemos de memoria (sobre todo la última).

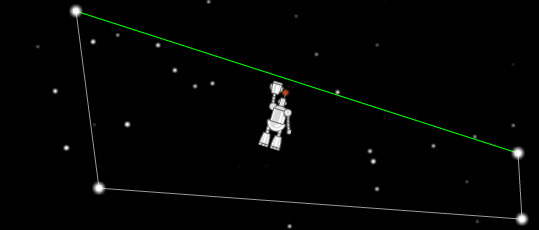
Ejemplo en funcionamiento: Puedes arrastrar el robot, o cualquiera de las cuatro estrellas que conforman los «bordes». El robot se encarará hacia el «borde» más cercano

• Ángulo entre dos puntos. Es muy sencillo de calcular gracias a la función atan2, una variante muy útil de la arcotangente y que se encuentra presente en la mayoría de lenguajes de programación (o librerías matemáticas, en su defecto). Cuidado con el único gotcha que tiene esta función, y es que se debe pasar como primer parámetro la coordenada y del punto, y como segundo la coordenada x, al contrario que en casi todas las demás funciones del universo conocido.

  
  		//ángulo en grados entre dos puntos
  		private function rotationDegreesTwoPoints(p1:Point, p2:Point):Number
  		{
  			return 180*Math.atan2(p2.y - p1.y, p2.x- p1.x)/Math.PI;
  		}
  
  

• Distancia entre dos puntos. La fórmula de la distancia euclídea debería ser de sobras conocida por todos. Tan sólo un apunte de optimización: si podemos, hemos de evitar computar la raíz cuadrada, ya que es una operación bastante costosa de calcular para el procesador. Por ejemplo, si lo que queremos es comparar distancias para ver qué elementos están más cerca o más lejos, no será necesario en absoluto computar las raíces cuadradas de todos los valores, ya que los órdenes relativos se mantienen al elevar al cuadrado. En notación matemática chapucera se podría expresar así:

  (x > y) <-> (x*x > y*y)

  Si queremos medir un radio de alcance o valor umbral para algún efecto, podemos operar todo el tiempo con el radio/umbral al cuadrado (pre calculado) para ahorrarnos la molesta raíz cuadrada.

  
    //elevar nuúmero al cuadrado (más rápido que pow)
    function sqr(x:Number):Number
    { 
      return x * x; 
    }
  		
    //Distancia enter dos puntos (al cuadrado)
    function distBetweenPointsSquared(v:Point, w:Point):Number
    { 
      return sqr(v.x - w.x) + sqr(v.y - w.y);
    }
  
  

• A partir de esta fórmula podemos construir otra que también resulta muy útil, Distancia entre punto y segmento. Como en el caso anterior, evitaremos computar la raíz cuadrada y devolveremos el valor de la distancia al cuadrado. Es bastante más complicada ya que tenemos que contemplar todas las posibilidades:

  
    //distancia mínima entre punto p y segmento vw
    function distToSegmentSquared(p:Point, v:Point, w:Point):Number
    {
      var longSeg:Number = distBetweenPointsSquared(v, w);
  
      if (longSeg == 0) return distBetweenPointsSquared(p, v);
  
      var t:Number = ((p.x - v.x) * (w.x - v.x) + (p.y - v.y) * (w.y - v.y)) / longSeg;
  
      if (t < 0) return distBetweenPointsSquared(p, v);
  
      if (t > 1) return distBetweenPointsSquared(p, w);
  
      return distBetweenPointsSquared(p, 
        new Point(
          v.x + t * (w.x - v.x),
          v.y + t * (w.y - v.y)) 
        );
    }
  

Aunque las funciones que presento están en ActionScript 3, son triviales de portar a otros lenguajes con sintaxis similar como JavaScript, Java o C++. ¡Espero que os resulten útiles!

Etiquetas: as3, game-development, geometría, matemáticas, tips